欢迎来到树的世界
在计算机科学中,树 (Tree) 是一种至关重要的数据结构,它精妙地模拟了自然界与社会中的层级关系。想象一下家族谱系、公司组织架构或是文件系统的目录结构——它们都可以用树来清晰地表示。
树由节点 (Nodes) 和连接节点的边 (Edges) 构成,形成一个无环的连通图。这种结构使得树在信息表示、数据组织、高效搜索与算法实现等众多领域大放异彩。本页面将引领您深入探索树的迷人世界,从基本概念到高级应用,为您揭开数据结构的奥秘。
核心名词解析
要深入理解树,掌握其核心术语是第一步。点击下方卡片即可翻转查看每个名词的详细解释与生动示例:
根节点 (Root)
根节点 (Root)
树的最顶层节点,独一无二,没有父节点。它是所有其他节点的祖先。
示例: 在文件系统中,驱动器(如 C:\)或根目录(/)就是根节点。
父节点 (Parent)
父节点 (Parent)
对于树中任意一个非根节点,直接连接其上层的那个节点即为其父节点。每个节点(除根外)有且仅有一个父节点。
示例: 在 `C:\Users\Documents` 路径中,`Users` 是 `Documents` 的父节点。
子节点 (Child)
子节点 (Child)
一个节点直接连接其下层的节点称为其子节点。一个节点可以有零个或多个子节点。
示例: 在 `Users` 文件夹下,`Documents`、`Downloads` 等文件夹都是 `Users` 的子节点。
兄弟节点 (Sibling)
兄弟节点 (Sibling)
拥有同一个父节点的多个节点互称为兄弟节点。它们位于树的同一层级。
示例: `Documents` 和 `Downloads` 文件夹(如果都在 `Users` 下)互为兄弟节点。
叶节点 (Leaf)
叶节点 (Leaf)
没有任何子节点的节点称为叶节点,也叫终端节点。它们是树枝的末梢。
示例: 文件系统中的文件(如 `report.docx`)通常是叶节点,它们不再包含其他项目。
内部节点 (Internal Node)
内部节点 (Internal Node)
至少拥有一个子节点的节点称为内部节点或非终端节点。根节点(如果它有子节点)也是内部节点。
示例: 包含文件或子文件夹的文件夹(如 `Users`, `Documents`)都是内部节点。
节点的度 (Degree)
节点的度 (Degree)
一个节点拥有的子树数量,即其直接子节点的个数。叶节点的度为 0。
示例: 如果一个文件夹内有 3 个子文件夹或文件,则该文件夹节点的度为 3。
树的高度/深度
树的高度/深度 (Height/Depth)
树的高度是其最长路径的长度(边的数量),通常从根到最远的叶节点。根节点的深度定义为 0,其子节点深度为 1,以此类推。树的高度等于最深节点的深度。
示例: 路径 `C:\Users\Documents\report.docx` 中,若 `C:\` 深度为 0,则 `report.docx` 深度为 3。若这是最长路径,则树高为 3。
子树 (Subtree)
子树 (Subtree)
树中任意一个节点及其所有后代(子孙)节点所构成的结构,本身也构成一棵完整的树。
示例: `Documents` 文件夹及其内部所有文件和子文件夹,共同构成了以 `Documents` 为根节点的一个子树。
动态构建演示
通过调整下方参数生成不同形态的树结构。点击树中的节点,可在右侧信息面板查看其详细属性及与树的关系。树的显示会自动缩放以适应容器。
树信息
选中节点信息
常见树类型
树的世界丰富多彩,演化出了适应不同需求的变体。了解这些常见类型及其特性,有助于我们选择合适的数据结构解决实际问题:
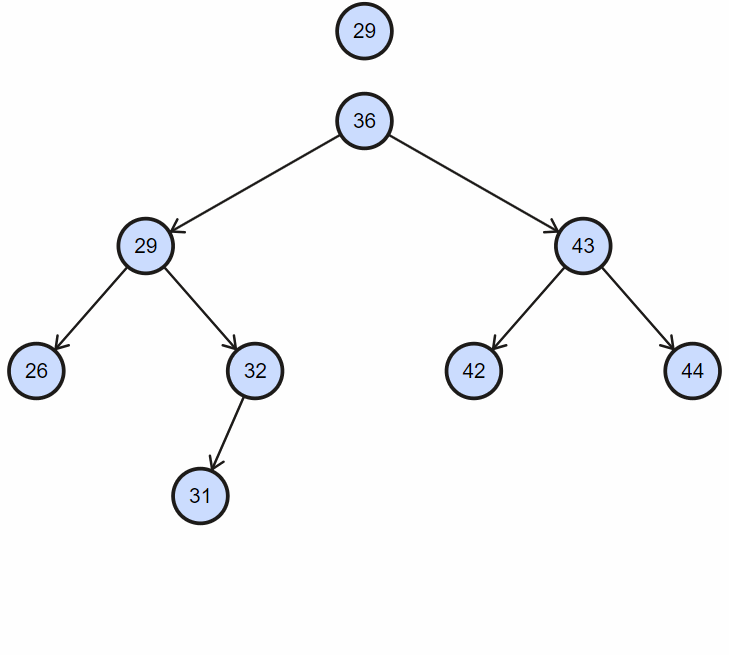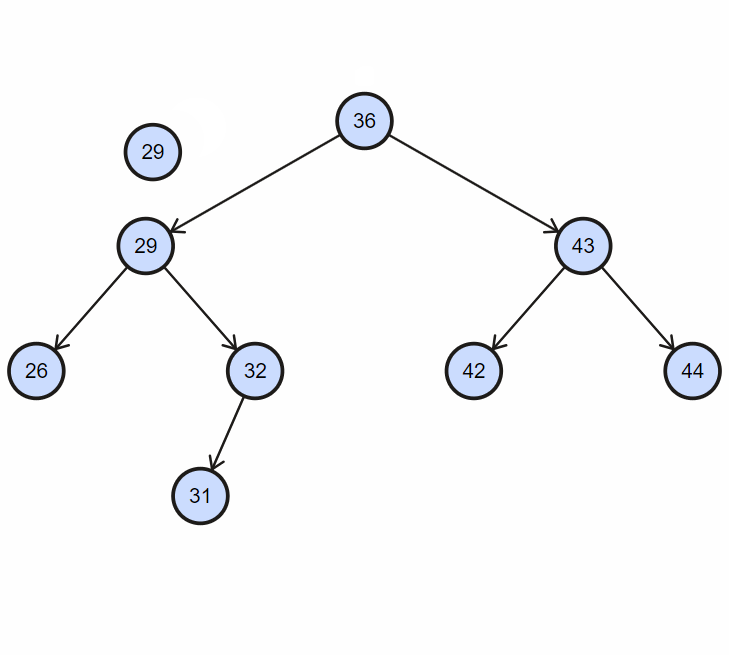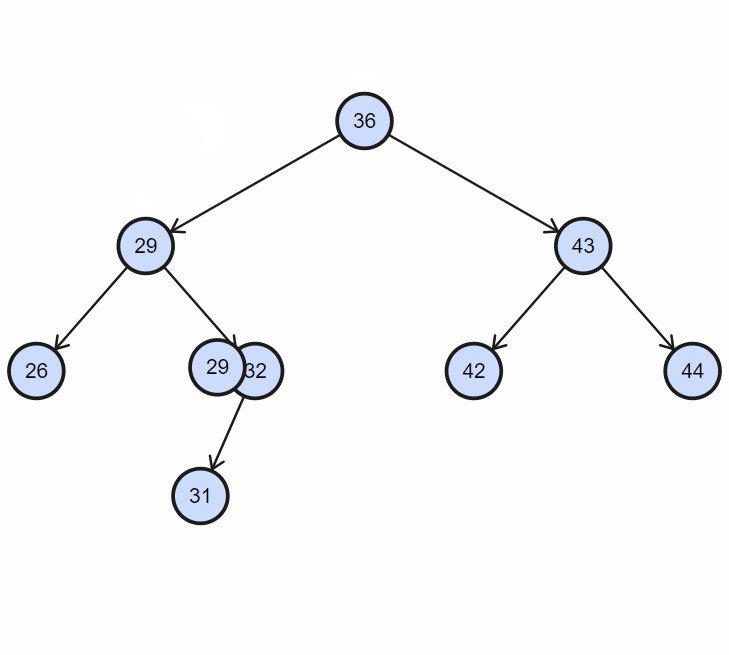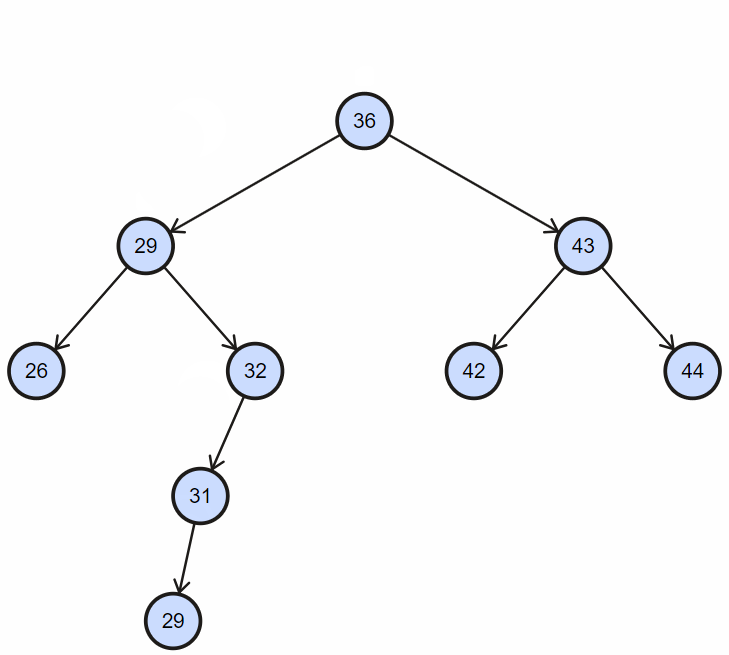
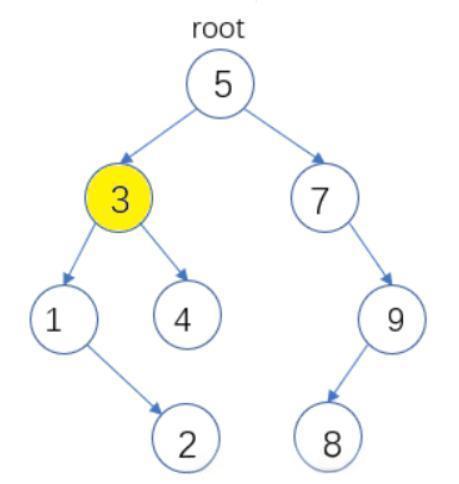
二叉搜索树 (BST)
每个节点最多有两个子节点(左和右)。关键特性是:左子树所有节点值小于父节点,右子树所有节点值大于父节点。这使得查找、插入和删除操作平均效率很高。
应用: 快速查找、排序基础、集合实现。
AVL 树
一种严格的自平衡二叉搜索树。它通过旋转操作确保任何节点的左右子树高度差不超过1。这保证了即使在最坏情况下,操作时间复杂度也是 O(log n)。
应用: 对查找性能要求极高且稳定的场景,如某些数据库索引。

红黑树
另一种流行的自平衡二叉搜索树。通过节点颜色(红或黑)和一组规则来维持大致平衡。相比AVL树,它允许稍大的高度差,但在插入和删除时调整(旋转)次数通常更少,综合性能优异。
应用: C++ STL (map, set), Java (TreeMap, TreeSet), Linux 内核。
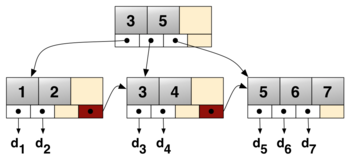
B 树 / B+ 树
为磁盘等慢速外存设计的多路搜索树。节点可以有多个子节点(阶数远大于2)。B+ 树是其常用变体,所有数据存在叶节点,叶节点间用指针连接,便于范围查询。
应用: 文件系统索引 (NTFS, HFS+), 数据库索引 (MySQL InnoDB, Oracle)。
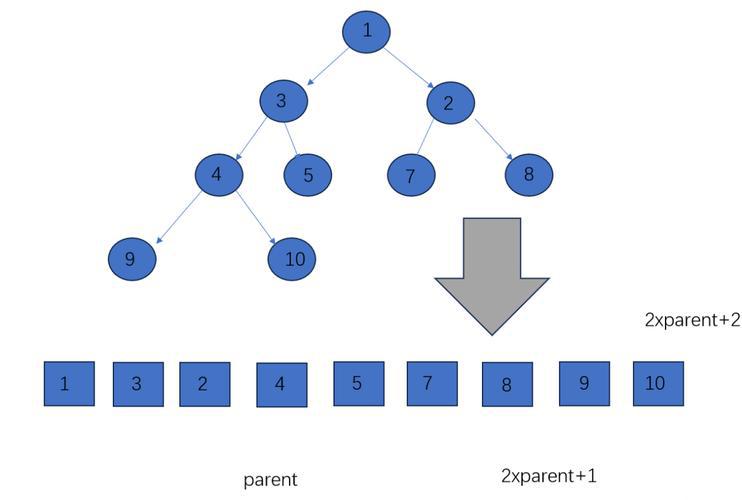
堆 (Heap)
通常指二叉堆,是一种特殊的完全二叉树,满足堆属性:父节点的值总是大于等于(最大堆)或小于等于(最小堆)其子节点的值。常用于实现优先队列。
应用: 优先队列、堆排序、图算法(Dijkstra, Prim)。
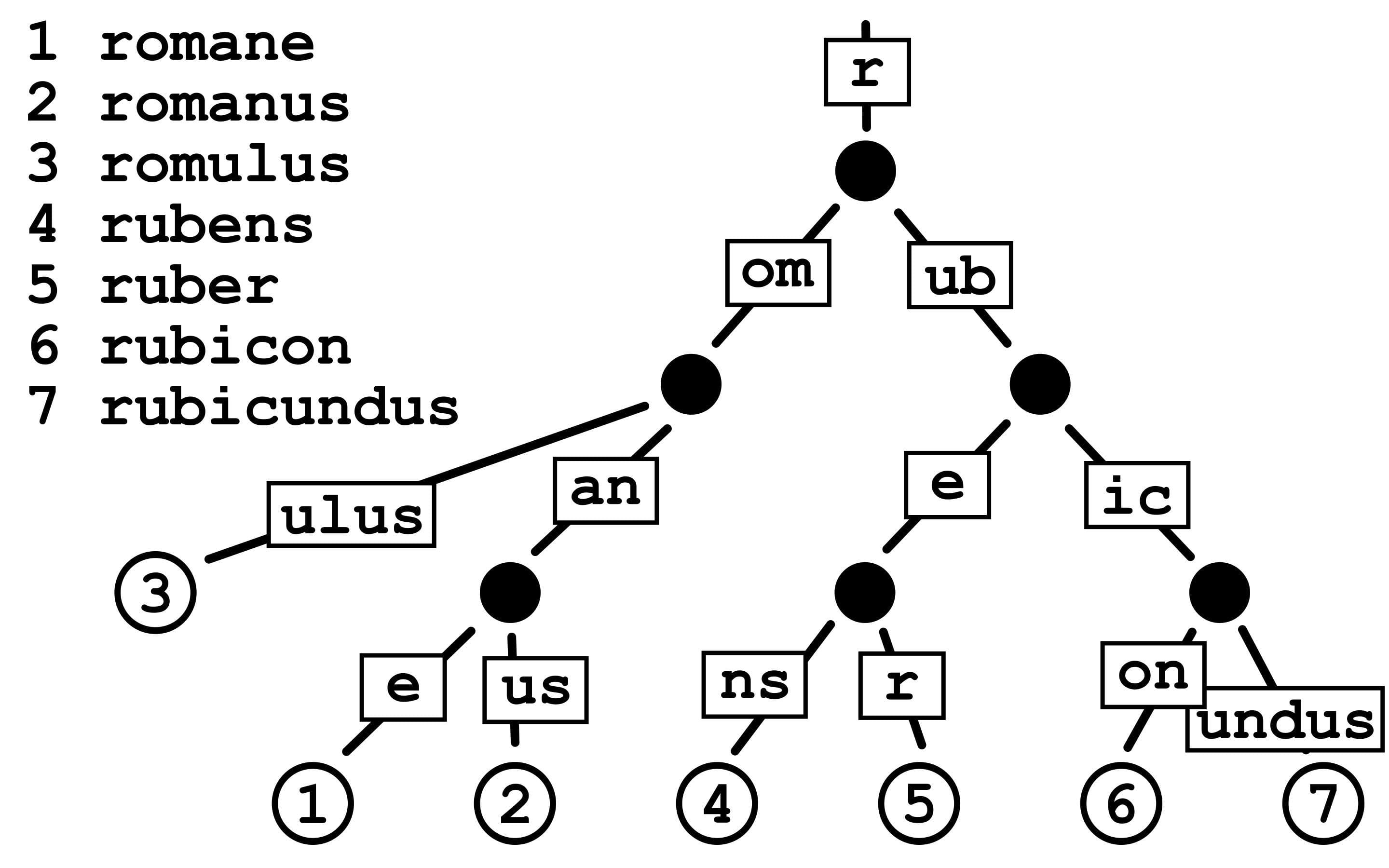
字典树 (Trie)
也称前缀树,专门用于高效存储和检索字符串集合。树的每条边代表一个字符,从根到一个节点的路径构成一个字符串或前缀。
应用: 搜索引擎自动补全、IP路由最长前缀匹配、拼写检查。
特性对比分析
不同的树结构各有千秋,适用于不同的场景。下表清晰对比了几种常见树的关键特性,助您快速把握它们的核心差异。点击表头可进行排序:
| 树类型 | 自平衡 | 查找(Avg) | 插入(Avg) | 删除(Avg) | 查找(Worst) | 主要应用场景 |
|---|---|---|---|---|---|---|
| 二叉搜索树 (BST) | 否 | O(log n) | O(log n) | O(log n) | O(n) | 基础查找/排序, 简单集合 |
| AVL 树 | 是 (严格) | O(log n) | O(log n) | O(log n) | O(log n) | 查找性能要求稳定且高 |
| 红黑树 | 是 (近似) | O(log n) | O(log n) | O(log n) | O(log n) | 通用库(map/set), 综合性能 |
| B/B+ 树 | 是 | O(logm n) | O(logm n) | O(logm n) | O(logm n) | 数据库/文件系统索引(减IO) |
| 堆 (Heap) | 结构特性 | O(n) | O(log n) | O(log n) (根) | O(n) | 优先队列, 堆排序 |
| 字典树 (Trie) | 否 | O(L) | O(L) | O(L) | O(L) | 字符串/前缀查找, 自动补全 |
注: L 代表字符串长度, m 代表 B/B+ 树的阶数。